Иоганн Кеплер – немецкий естествоиспытатель, математик, астроном, астролог, оптик и протестантский богослов, открывший законы движения планет, названные в его честь «законами Кеплера». Как и его коллега Галилео Галилей, Иоганн Кеплер развил гелиоцентрическое мировоззрение, основанное ещё Коперником. Его новаторские идеи намного опередили своё время.
К сожалению, ученый прожил не слишком длинную и очень нелегкую жизнь. Несмотря на это, он обогатил науку потрясающими достижениями, потребовавшими не только гениальных озарений, но и многолетнего изнурительного труда, масштаб которого удивляет и сегодня.

Портрет Кеплера в 1620 г., автор неизвестен
Детство Кеплера, родившегося 27 декабря 1571 года в городке Вейль неподалеку от Штутгарта, нельзя назвать безоблачным. Семья жила небогато, к тому же он рос практически без отца, который неоднократно нанимался ландскнехтом в чужеземные армии и исчез насовсем, когда Гансу было всего 16 лет. Детей воспитывала мать Катарина, дочь владельца деревенской гостиницы, женщина неуживчивая, сварливая и совершенно необразованная. Гансу светила совершенно ординарная жизнь, но судьба рассудила иначе. Мальчик не вылезал из болезней (оспа, в результате которой сильно ослабло его зрение, несварение желудка, мигрени) и не годился для физической работы. Но голова у него действовала отлично. В семь лет Ганс поступил в начальную немецкую школу, откуда перешел в латинское училище. В 13-летнем возрасте он выдержал конкурсный экзамен, открывший доступ к духовному образованию. Юноша блестяще окончил семинарии первой и второй ступени и осенью 1589 года стал студентом Тюбингенского университета.
В Тюбингене Кеплер провел около пяти лет. За два года он прошел курс факультета свободных искусств и получил степень магистра. Одним из его наставников был Михель Мёстлин — автор довольно известного учебника по астрономии и верный последователь Коперника. Под руководством Мёстлина Кеплер изучил труды греческих геометров, арифметику, тригонометрию и начатки алгебры. Он постиг также тонкости птолемеевской и коперниканской космологии и стал убежденным сторонником гелиоцентрической системы. Однако о занятиях наукой юноша не помышлял и собирался продолжать образование на богословском факультете, куда поступил в 1591 году. Перед этим университетский сенат испросил городские власти Вейля сохранить Кеплеру стипендию на весь оставшийся срок обучения. «Юный Кеплер, — писали профессора, — наделен таким выдающимся умом, что от него можно ожидать незаурядных достижений».
Однако духовной карьере Кеплера не суждено было состояться. 13 марта 1594 года его как лучшего выпускника отправили в австрийский город Грац, чтобы срочно заменить скончавшегося учителя математики в лютеранской школе.
Шло время. Кеплер обжился в Граце и смирился со своей новой профессией. Все шло к тому, что он так и останется отлично образованным, но все же вполне рядовым преподавателем провинциальной школы. К счастью для мировой науки, судьба решила иначе. 19 июля 1595 года свершилось событие, которое радикально изменило жизнь Кеплера и вывело его на дорогу великих открытий в физике и астрономии.
Все началось с урока, в ходе которого Кеплер объяснял движение Юпитера и Сатурна по небесной сфере. Каждые 20 лет эти планеты сближаются в поясе зодиакальных созвездий — Юпитер нагоняет Сатурн, а потом уходит вперед (эти встречи имели место в 1563 и 1583 годах и должны были произойти в 1603, 1623 и 1643). С незапамятных времен астрономы и астрологи замечали, что зоны такого сближения каждый раз смещаются в зодиакальном поясе чуть меньше чем на треть полного круга. Кеплер начертил на доске окружность, расположил на ней на равных расстояниях 12 зодиакальных созвездий и отметил несколько сближений Юпитера и Сатурна, начав 1583 годом.
И вот что вышло. Если соединить три последовательных сближения отрезками, получается правильный треугольник, вписанный в зодиакальную окружность. Повторение этой операции дает такой же треугольник, только несколько повернутый (поскольку смещение все же не доходит до 120 градусов). Если продолжать дальше, середины сторон всех получающихся треугольников очертят окружность вдвое меньшего радиуса по сравнению с той, в которую они вписаны. Тут Кеплера осенило. Он знал, что согласно книге Коперника «Об обращении небесных сфер» радиус орбиты Сатурна примерно в 1,75 раза превышает юпитерианский. А эта величина слишком близка к отношению радиусов внешней и внутренней окружностей 2:1, чтобы счесть ее случайным совпадением. А вдруг соотношения между параметрами планетных орбит определяются свойствами определенных геометрических объектов? Позднее Кеплер вспоминал, что это озарение привело его в состояние восторга, которое невозможно передать словами.
Это было лишь начало. Кеплер быстро осознал, что с помощью плоских фигур устройство планетной системы понять невозможно, необходимы объемные тела. Еще античным математикам были известны пять правильных многогранников: четырехгранный тетраэдр, шестигранный куб, восьмигранный октаэдр, 12-гранный додекаэдр и 20-гранный икосаэдр. Кеплер решил, что они укладываются в структуру, которая определяет, как число планет (тогда их было известно всего шесть!), так и их орбитальные параметры. Это шесть концентрических сфер, из которых пять содержат вписанные многогранники. Первая, внешняя сфера соответствует орбите Сатурна. В нее вложен куб, а в него — вторая сфера, сфера Юпитера. В эту сферу вписан тетраэдр, в котором расположена сфера Марса. Двигаясь к центру системы, мы пересечем додекаэдр, содержащий вписанную земную сферу, икосаэдр со сферой Венеры и, наконец, октаэдр со сферой Меркурия. Она не содержит вписанных тел, а в ее центре находится Солнце.
Уже в октябре Кеплер начал писать книгу с изложением своей системы. Этот труд несколько месяцев печатался в Тюбингене и был окончательно сброшюрован в марте 1597 года. Его длиннейший заголовок обычно дают в сокращенном варианте: Mysterium cosmographicum — «Тайна мироздания».
Кеплер сам отправил монографию нескольким видным астрономам. Одна из копий через третьи руки попала к не слишком известному профессору математики Падуанского университета Галилео Галилею, который отозвался на нее весьма доброжелательным письмом (правда, в основном его обрадовало, что у теории Коперника появился еще один сторонник). Кеплер отправил свой труд и первому астроному Европы датчанину Тихо Браге, который счел упражнения с многогранниками остроумными, но совершенно спекулятивными. Однако в сильно задержавшемся ответном письме Браге дал понять, что готов ознакомить Кеплера со своим обширным архивом наблюдений движений планет, произведенных в лучшей в мире обсерватории на острове Гвен вблизи Копенгагена. Для Кеплера это приглашение оказалось воистину судьбоносным, хоть воспользовался он им далеко не сразу.
Публикация «Тайны мироздания» сделала Кеплера астрономом с именем. Через четверть века он писал, что эта небольшая книга дала толчок всем его последующим исследованиям. И было там по-настоящему революционное озарение, которое современники практически не заметили. Кеплер — первым в мире! — пришел к заключению, что все планеты подвержены силовому воздействию со стороны Солнца, которое и заставляет их двигаться по орбитам. Эта идея не соответствует принципам ньютоновской динамики (планеты движутся по инерции, а солнечное притяжение лишь искривляет их пути), но она навела Кеплера на очень плодотворные заключения. Из нее следовало, что планеты должны двигаться тем быстрее, чем они ближе к Солнцу, — ведь разгоняющая их сила возрастает по мере приближения к светилу. Через несколько лет логика этого рассуждения помогла Кеплеру открыть законы планетных движений.
Осенью 1598 года в Штирии начались гонения на протестантов. Кеплеру вместе с многими единоверцами пришлось покинуть Грац, но через месяц ему в виде исключения позволили вернуться и продолжить работу в качестве окружного математика. Тем не менее из-за изгнания ректора и почти всех учителей занятия в школе прекратились. Кеплеру стало ясно, что будущего в Граце у него нет. Он предпринимал лихорадочные попытки найти место за пределами Австрии, но безуспешно.

Портрет Кеплера неизвестного художника 17 века. Галерея Уффици, Флоренция
И тут помог Тихо Браге, который к этому времени стал придворным математиком императора Священной Римской империи и короля Богемии Рудольфа II. В декабре 1599 года Браге вторично пригласил Кеплера в целях совместной работы. Еще до получения этого письма Кеплер отправился в имперскую столицу Прагу в надежде стать ассистентом Браге. 4 февраля ученые встретились, и после этого свидания их жизненные линии уже не расплетались, хотя личные отношения оказались очень непростыми. Браге попросил императора взять Кеплера на службу, дабы тот смог обработать его архивы и составить на их основе самые совершенные таблицы планетных движений. Эти таблицы Браге предложил назвать в честь императора — Рудольфовыми. План монарху понравился, и он дал согласие.

Кеплер и император Рудольф II. Гравюра Ф. Бюло, 1862г
Первоначально предполагалась, что для Кеплера создадут специальную должность. Однако вскоре Тихо Браге скоропостижно скончался (среди причин смерти назывались и детективные версии). Через два дня после похорон Браге Кеплера назначили придворным математиком с годовым окладом 500 флоринов. Правда, императорская казна перманентно пустовала и Кеплеру хронически не доплачивали. Однако он получил часть архива Браге — ту, которая относилась к движениям Марса. Эти материалы и легли в основу кеплеровской теории планетных движений, обессмертившей имя своего создателя.
Кеплер прожил в Праге 11 лет — самых спокойных и плодотворных. Там он написал свой главный астрономический труд. Сначала Кеплер хотел назвать его «Марсианскими комментариями», но потом придумал заголовок посложнее — «Новая астрономия, обоснованная в соответствии с ее причинами, или Небесная физика, изложенная посредством комментариев к движениям Марса, вычисленных на основе наблюдений благородного мужа Тихо Браге». Именно эта книга была напечатана в судьбоносном для астрономии 1609 году.
Анализ марсианских движений Кеплер начал с Земли. И это естественно, ведь именно с этой движущейся космической платформы Тихо Браге определял небесные координаты и Марса, и остальных планет. На основании этих измерений Кеплер показал, что Земля то приближается к Солнцу, то удаляется от него. В соответствии с теорией, изложенной еще в «Тайне мироздания», отсюда следует, что скорость орбитального движения Земли уменьшается вдали от Солнца и возрастает по мере приближения к светилу. Именно эту закономерность Кеплер и выявил, обрабатывая результаты Тихо Браге.
Этот вывод позволил ученому по-новому понять движение Марса. Уже античные астрономы знали, что Марс движется по небосводу с переменной скоростью. Объяснение было таким: и Марс, и прочие планеты совершают комбинации круговых движений, скорости которых строго постоянны, поэтому наблюдаемая переменная скорость — всего лишь видимость. А вот с точки зрения Кеплера, непостоянство скорости Марса совершенно реально и объясняется тем, что эта планета, как и Земля, изменяет свое расстояние от Солнца. Кроме того, Кеплер убедился, что Земля движется вполне аналогично Марсу, то есть является обычной планетой. Это был сильный аргумент в пользу гелиоцентрической теории Коперника, которая в те времена отнюдь не пользовалась всеобщим признанием (в частности, ее не разделял Тихо Браге).
Кеплер поначалу исходил из того, что Земля движется по окружности, центр которой находится не слишком далеко от Солнца. Эта рабочая гипотеза позволила описать изменчивость планетарной скорости Земли в виде простого математического правила: радиус-вектор планеты (отрезок, соединяющий ее с Солнцем) за равные промежутки времени зачерчивает равные площади. В списке законов Кеплера это правило значится под вторым номером, хотя исторически было установлено раньше прочих, в самом конце 1601 или в начале 1602 года.
Второй закон Кеплера следует из того, что орбитальное движение планеты не меняет ее момента количества движения. Сей факт прямо следует из ньютоновской динамики, но Кеплеру, конечно, он не был известен. Свой закон площадей Кеплер фактически угадал, а если и обосновал, то весьма приблизительно. Однако проверка на им же вычисленных параметрах земной орбиты подтвердила, что это правило хорошо соблюдается.
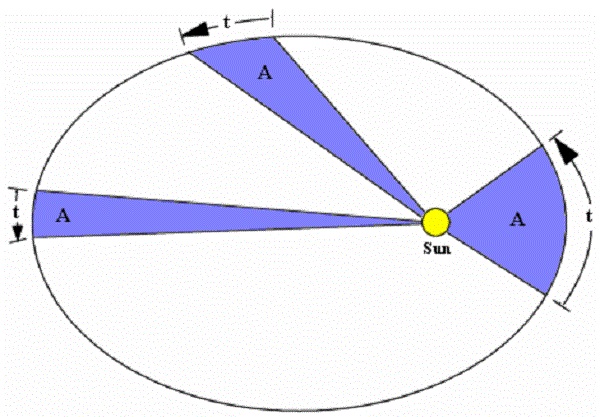
Второй закон Кеплера: закрашенные площади равны и проходятся за одинаковое время
Судя по всему, Кеплер в ходе работы над «Новой астрономией» все же не уверился в нем до конца; во всяком случае, он не утверждает его истинности открытым текстом. Математическое доказательство закона площадей дал только Исаак Ньютон. Наверное, не лишне заметить, что этому закону подчиняются любые тела, движущиеся в центральном поле тяготения, даже если они перемещаются по разомкнутым траекториям. Более того, силовой потенциал вовсе не обязан соответствовать ньютоновскому закону обратных квадратов — достаточно, если он зависит только от расстояния до центра силы. Так что второй закон Кеплера обладает куда большей общностью, нежели предполагал его первооткрыватель!

«Кубок Кеплера»: модель Солнечной системы из пяти платоновых тел
Самым крепким орешком оказалось определение формы марсианской орбиты. С помощью крайне трудоемких вычислений Кеплер установил, что она никак не может быть окружностью. Сначала Кеплер решил, что Марс движется по овалу, потом попробовал нечто вроде сечения яйца, но все эти фигуры явно не соответствовали наблюдениям Тихо Браге. В конце концов Кеплер увидел, что отношение минимального и максимального расстояний между Марсом и Солнцем отличается от единицы на величину, равную половине квадрата орбитального эксцентриситета (отношения дистанции между Солнцем и центром орбиты к ее радиусу). Именно такое соотношение должно выполняться, если орбита — правильный эллипс (в предположении, что эксцентриситет много меньше единицы). Выходило, что Марс движется по эллипсу, в одном из фокусов которого расположено Солнце. Если это утверждение обобщить на остальные планеты, получается первый закон Кеплера. Правда, такое обобщение Кеплер сформулировал позднее, но, судя по всему, считал так с самого начала.
Кеплер окончательно пришел к концепции эллиптической орбиты Марса весной 1605 года. После этого он всего за несколько месяцев закончил рукопись «Новой астрономии» (книга вышла лишь спустя четыре года, но на то были ненаучные причины).
Публикация этой книги принесла Кеплеру европейскую известность. Правда, его результаты признали далеко не все — например, их так и не принял (а возможно, и не понял) великий Галилей. Но такова судьба едва ли не всех великих открытий.
А жизнь продолжалась — и не всегда удачно. Умерла жена, оставив Кеплера с двумя маленькими детьми. Незадолго до этого с престола был смещен покровитель Кеплера Рудольф II. Осложнились отношения с лютеранскими священниками, которые заподозрили его в сочувствии кальвинизму. Из-за этого Кеплер не смог получить работу в Вюртемберге, куда хотел вернуться. После длительных переговоров Кеплеру предложили место математика в Линце, столице Верхней Австрии, на условиях, что он продолжит работу над таблицами планетных движений и займется местной картографией. Кеплер перебрался в Линц в 1612 году и прожил там 14 с половиной лет. Там он повторно женился, и супруга родила ему семерых детей.
На годы жизни в Линце пришелся длительный процесс по обвинению матери Кеплера в колдовстве, и ее защита отняла у ученого много здоровья и душевных сил. К тому же весной 1618 года началась Тридцатилетняя война, со временем захлестнувшая и Верхнюю Австрию.
Но Кеплер работал — и как работал! В 1619 году он опубликовал свой любимый труд «Пять книг гармонии мира». Об астрономии в нем говорится немного, больше о геометрии и философии. Однако именно на страницах этой книги появился третий закон Кеплера, который он открыл 15 мая 1618 года.
В 1617—1621 годах увидел свет публиковавшийся по частям самый обширный труд Кеплера «Очерки коперниканской астрономии», первый в мире учебник с детальным описанием гелиоцентрической модели мира. В этой книге законы планетных движений представлены как общие принципы, которым подчиняются все планеты; там же приведены результаты вычислений, с помощью которых Кеплер определил орбитальные параметры Меркурия, Венеры, Юпитера и Сатурна. В этой монографии впервые появился термин «инерция» — правда, не в том понимании, что сложилось после работ Галилея и Ньютона.
В конце пребывания в Праге после изнурительных переговоров с наследниками Тихо Браге Кеплер получил в свое распоряжение весь архив его наблюдений и у него наконец-то появилась возможность вплотную впрячься в составление астрономических таблиц, ради которых его взял на службу покойный Рудольф II. Эта исполинская работа была завершена во второй половине 1624 года.

Памятник Кеплеру в Линце
Эпилог
Выпустив в свет «Рудольфовы таблицы», Кеплер выполнил обязательства перед имперским правительством. Ученый мог остаться в прежней должности императорского математика ценой перехода в католичество, но решительно от этого отказался. Он готов был переехать в Англию, но в конце концов согласился пойти на службу математиком к австрийскому военачальнику Альбрехту Валленштейну.
В августе 1630 года Валленштейн был смещен со своего высокого поста, так и не выплатив Кеплеру обещанного жалованья. В надежде получить хоть часть причитавшихся денег Кеплер в октябре отправился в Регенсбург, где заседал имперский сейм. Он добрался туда вконец простуженным и 15 ноября скончался. На не сохранившемся до наших дней надгробии была выбита латинская эпитафия, сочиненная самим Кеплером:
Mensus eram coelos; nunc terrae meteor umbras;
mens coelestis erat; corporis umbra jacet.
Я небеса измерял, ныне тени Земли измеряю.
Дух мой на небе жил, здесь же тень тела лежит.
В публикации использованы материалы popmech.

 Онлайн
Онлайн



