Пользователи фотоаппаратов знают, что ближе к краям даже на очень хорошем объективе фотографии могут страдать от существенного снижения резкости. Вседело в законах оптики — еще древнегреческий математик Диокл в своей работе «О зажигательных зеркалах» сформулировал проблему, которую человечество не могло полностью преодолеть более двух тысяч лет.
Дело в том, что линзы сделаны из сферических поверхностей и чем дальше световые лучи отклоняются от оптической оси линзы или падают на неё под углом, тем сильнее не совпадает фокус таких лучей из-за разницы в преломлении света. В результате центр получаемой картинки получается резче, чем края — это называется «сферическая аберрация».
В своей работе 1690 года «Трактат о свете» астроном Кристиан Гюйгенс отметил, что Исаак Ньютон и Готфрид Лейбниц пытались решить эту проблему созданием особых линз для фиксированного расстояния фокусировки, но не смогли. Стоит упомянуть, что Ньютон изобрел телескоп, который был избавлен от проблемы хроматической аберрации, но не сферической.
В своей статье 1949 года Г. Д. Вассерман и Э. Вольф предложили апланатическую линзу, основанную на интеграле, который они нашли численными методами. Их решение было приближением с помощью подбора на компьютере, а не окончательным, и включало использование асферических элементов, которые сложнее изготовить достаточно точно. Заодно была сформулирована проблема Вассермана-Вольфа. Благодаря этому многие современные объективы включают асферические линзы для коррекции сферической аберрации, создавая сложные оптические группы. Полноценное решение этой проблемы помогло бы улучшить оптические системы везде: от очков и камер в смартфонах до телескопов и микроскопов.
Наконец, в 2018 году докторант Национального автономного университета Мексики (НАУ) Гектор Чапарро-Ромо (Héctor Chaparro-Romo), пытавшийся решить проблему в течение 3 лет, привлек себе на помощь докторанта Рафаэля Гонсалеса-Акунью (Rafael González-Acuña) из Монтеррейского технологического института.
Поначалу Гонсалес не хотел тратить силы на проблему, которую не могли решить тысячелетиями. Но по настоянию Гектора Чапарро решил принять вызов. Как вспоминал затем Рафаэль Гонсалес, после нескольких месяцев работы, произошел прорыв: «Я помню, как однажды утром готовил себе кусочек хлеба с Нутеллой и внезапно произнес вслух: «Эврика! Вот и решение!»». Затем он побежал к компьютеру и начал вводить программный код идеи. Когда исследователь выполнил симуляцию и увидел, что та работает, он буквально пустился вскачь. После этого дуэт провeл ещe ряд симуляций и рассчитал эффективность метода с 500 лучами — в результате средний результат для всех примеров составил 99,99999999999 %. То есть разница в резкости на всей плоскости кадра составила ничтожные 0,0000000001 %.

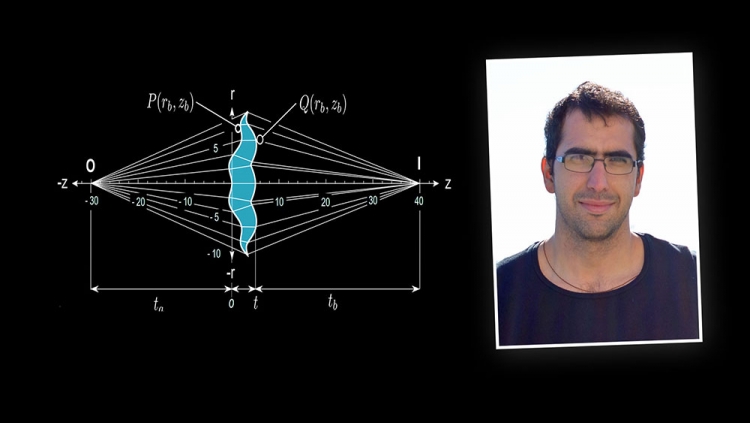
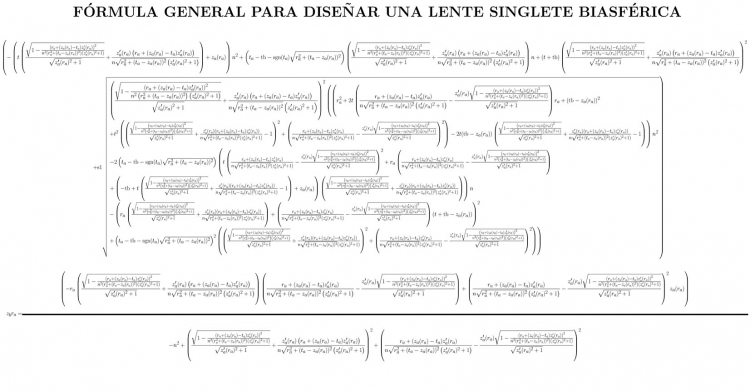
Результаты работы были опубликованы в статье «Общая формула дизайна биасферических синглетных линз без сферической аберрации» в научном журнале «Прикладная оптика». Приведённое изображение показывает полученное учеными общее алгебраическое уравнение замкнутой формы для конструкции сферической линзы без аберраций. Она описывает зависимость формы второй асферической поверхности конкретной линзы от первой поверхности и фокусного расстояния. Вторая асферическая поверхность призвана устранить все аберрации, создаваемые первой поверхностью. Формула решает проблему Вассермана-Вольфа, сформулированную аналитически в 1949 году, но известную учёным около двух тысяч лет.
В рамках того же исследования Рафаэль Г. Гонсалес-Акунья, Гектор А. Чапарро-Ромо и Хулио Гутьеррес Вега (Julio Gutiérrez Vega) также опубликовали в журнале «Прикладная оптика» статью «Общая формула для создания синглетной линзы произвольной формы без сферической аберрации и астигматизма», в которой они дают аналитическое решение Проблемы Леви-Чивиты, сформулированной в 1900 году.
В результате мы можем надеяться, что в скором времени появятся объективы, избавленные от проблемы сферической аберрации. Причем производство новых линз в теории должно быть дешевле. Впрочем, вряд ли стоит ожидать, что первые такие объективы будут стоить меньше.
Источник – 3dnews.

 Онлайн
Онлайн



